Optical Flow on Evolving Sphere-Like Surfaces
Lukas F. Lang and Otmar Scherzer
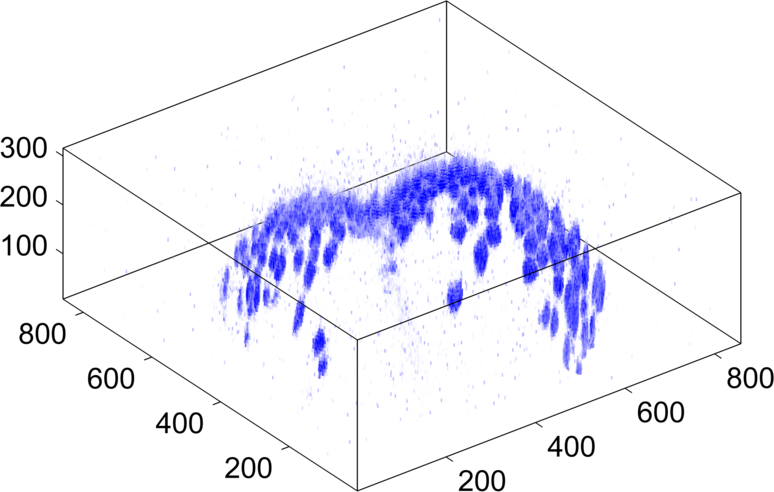 |
 |
 |
Abstract
In this work we consider optical flow on evolving Riemannian 2-manifolds which can be parametrised from the 2-sphere. Our main motivation is to estimate cell motion in time-lapse volumetric microscopy images depicting fluorescently labelled cells of a live zebrafish embryo. We exploit the fact that the recorded cells float on the surface of the embryo and allow for the extraction of an image sequence together with a sphere-like surface. We solve the resulting variational problem by means of a Galerkin method based on vector spherical harmonics and present numerical results computed from the aforementioned microscopy data.
BibTeX
@article{LanSch17, author = {Lang, L.~F. and Scherzer, O.}, title = {Optical flow on evolving sphere-like surfaces}, doi = {10.3934/ipi.2017015}, journal = {Inverse Problems and Imaging}, number = {2}, pages = {305--338}, volume = {11}, year = {2017} }
Paper: Preprint
Data
Code
Download: https://bitbucket.org/lukaslang/ofish
Dependency: https://bitbucket.org/lukaslang/ofd
Acknowledgements
We thank Pia Aanstad from the University of Innsbruck for sharing her biological insight and for kindly providing the microscopy data. Moreover, we are grateful to Peter Elbau and Clemens Kirisits for their helpful comments, and to Jose A. Iglesias for carefully proofreading an earlier version of this article and providing valuable feedback. This work has been supported by the Vienna Graduate School in Computational Science (IK I059-N) funded by the University of Vienna. In addition, we acknowledge the support by the Austrian Science Fund (FWF) within the national research network "Geometry + Simulation" (project S11704, Variational Methods for Imaging on Manifolds). The majority of this article was written while Lukas F. Lang was employed by the Computational Science Center, University of Vienna, Austria.
